BLOQUE II. RESUELVES PROBLEMAS DE LÍMITES EN SITUACIONES DE CARÁCTER ECONÓMICO, ADMINISTRATIVO, NATURAL Y SOCIAL.
Desempeños del estudiante al concluir el bloque
Aplica el concepto de límite a partir de la resolución de problemas económicos, administrativos, naturales y sociales de la vida cotidiana.
Calcula límites a partir de la elaboración de gráficas en derive y su interpretación de las representaciones gráficas de funciones, mostrando habilidades en la resolución de problemas de
situaciones cotidianas.
Objetos de aprendizaje
Los límites: su interpretación en una tabla, en una gráfica y su aplicación en funciones algebraicas.
El cálculo de límites en funciones algebraicas y trascendentes.
Competencias a desarrollar
Interpreta gráficas de funciones continuas y discontinuas analizando el dominio y contradominio; y argumenta el comportamiento gráfico de la variable dependiente (y) en los punto (s) de discontinuidad.
Explica e interpreta los valores de una tabla, calcula valores cercanos a un número y analiza el comportamiento en los valores de la variable dependiente en problemas de su entorno social, económico y natural.
Explica e interpreta diferentes representaciones gráficas y determina límites que tienden a infinito positivo o negativo, a cero, limites laterales por la izquierda y por la derecha, y límites finitos, de los objetos naturales que lo rodean.
Argumenta la solución obtenida de un problema económico, administrativo, natural o social, mediante la teoría de los límites.
Valora el uso de la TIC's en el modelado gráfico y algebraico de los límites para facilitar u interpretación y simulación en la resolución de problemas presentes en su contexto.
Formula y resuelve problemas, a partir del cálculo de dominio y contradominio de las funciones algebraicas para determinar sus límites,
demostrando su habilidad en la resolución de problemas algebraicos.
Determina límites para funciones racionales, exponenciales, logarítmicas y trigonométricas.
El cálculo de límites en funciones algebraicas y trascendentes.
Competencias a desarrollar
Interpreta gráficas de funciones continuas y discontinuas analizando el dominio y contradominio; y argumenta el comportamiento gráfico de la variable dependiente (y) en los punto (s) de discontinuidad.
Explica e interpreta los valores de una tabla, calcula valores cercanos a un número y analiza el comportamiento en los valores de la variable dependiente en problemas de su entorno social, económico y natural.
Explica e interpreta diferentes representaciones gráficas y determina límites que tienden a infinito positivo o negativo, a cero, limites laterales por la izquierda y por la derecha, y límites finitos, de los objetos naturales que lo rodean.
Argumenta la solución obtenida de un problema económico, administrativo, natural o social, mediante la teoría de los límites.
Valora el uso de la TIC's en el modelado gráfico y algebraico de los límites para facilitar u interpretación y simulación en la resolución de problemas presentes en su contexto.
Formula y resuelve problemas, a partir del cálculo de dominio y contradominio de las funciones algebraicas para determinar sus límites,
demostrando su habilidad en la resolución de problemas algebraicos.
Determina límites para funciones racionales, exponenciales, logarítmicas y trigonométricas.
Límites (una introducción)
Aproximarse
A veces algo no se puede calcular directamente... ¡pero puedes saber cuál debe de ser el resultado si te vas acercando más y más!
Usemos por ejemplo esta función:
(x2-1)/(x-1)
Y calculemos su valor para x=1:
(12-1)/(1-1) = (1-1)/(1-1) = 0/0
¡Pero 0/0 es un problema! En realidad no podemos saber el valor de 0/0, así que tenemos que encontrar otra manera de hacerlo.
En lugar de calcular con x=1 vamos a acercarnos poco a poco:
| x | (x2-1)/(x-1) |
|---|---|
| 0.5 | 1.50000 |
| 0.9 | 1.90000 |
| 0.99 | 1.99000 |
| 0.999 | 1.99900 |
| 0.9999 | 1.99990 |
| 0.99999 | 1.99999 |
| ... | ... |
Vemos que cuando x se acerca a 1, (x2-1)/(x-1) se acerca a 2
Ahora tenemos una situación interesante:
- Cuando x=1 no sabemos la respuesta (es indeterminada)
- Pero vemos que va a ser 2
Queremos dar la respuesta "2" pero no podemos, así que los matemáticos usan la palabra "límite" para referirse exactamente a estas situaciones
El límite de (x2-1)/(x-1) cuando x tiende (o se aproxima) a 1 es 2
Y con símbolos se escribe así:
Así que es una manera especial de decir "ignorando lo que pasa al llegar, cuando te acercas más y más la respuesta se acerca más y más a 2"
En un gráfico queda así:
Así que en realidad no puedes decir cuánto vale en x=1.
Pero sí puedes decir que cuando te acercas a 1, el límite es 2.
|  |
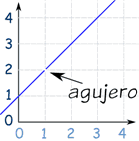¡Mira los dos lados!
Es como subir una colina y darte cuenta de que el camino ha "desaparecido" mágicamente...
... pero si sólo miras uno de los dos lados, ¿quién sabe qué está pasando?
¡Así que tienes que mirar las dos direcciones para estar seguro de dónde "debe de estar"!
|
Probemos por el otro lado:
| x | (x2-1)/(x-1) |
|---|---|
| 1.5 | 2.50000 |
| 1.1 | 2.10000 |
| 1.01 | 2.01000 |
| 1.001 | 2.00100 |
| 1.0001 | 2.00010 |
| 1.00001 | 2.00001 |
| ... | ... |
También va hacia 2, así que todo está bien
Cuando es distinto en los dos lados
Pero y si tenemos una función "f(x)" con un "salto" así:
 |
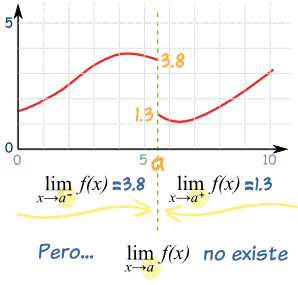¡En esta función el límite no existe en "a" ... !
No puedes decir cuál es, porque hay dos respuestas contradictorias:
Pero sí puedes usar los signos "-" o "+" (como en el dibujo) para definir los límites laterales:
Y el límite ordinario "no existe"
|
¿Los límites sólo son para funciones difíciles?
¡Los límites valen también cuando ya sabes el valor al llegar! Nadie ha dicho que sean sólo para funciones complicadas.
Por ejemplo:
Sabemos perfectamente que 10/2 = 5, pero también podemos usar límites (¡si queremos!)
Acercarse al infinito
 | El infinito es una idea muy especial. Sabemos que no podemos alcanzarlo, pero podemos calcular el valor de funciones que tienen al infinito dentro. |
Vamos a empezar con un ejemplo interesante.
| Pregunta: ¿Cuál es el valor de 1/∞? |
| Respuesta: ¡No lo sabemos! |
¿Por qué no lo sabemos?
La razón más simple es que infinito no es un número, es una idea. Así que 1/∞ es un poco como decir 1/belleza o 1/alto.
A lo mejor podríamos decir que 1/∞ = 0 ... pero eso es un poco problemático, porque si dividimos 1 en infinitas partes y resulta que cada una es 0, ¿qué ha pasado con el 1?
De hecho 1/∞ es indefinido.
¡Pero podemos acercarnos a él!
Así que en lugar de intentar calcular con infinito (porque no sacaremos ninguna respuesta razonable), vamos a probar con valores de x más y más grandes:
|  |
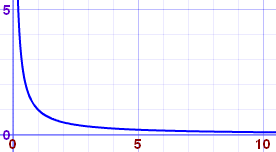Ahora vemos que cuando x crece, 1/x tiende a 0
Ahora tenemos una situación interesante:
- No podemos decir qué pasa cuando x llega a infinito
- Pero vemos que 1/x va hacia 0
Queremos decir que la respuesta es "0" pero no podemos, así que los matemáticos usan la palabra "límite" para referirse exactamente a esto
El límite de 1/x cuando x tiende a infinito es 0
Y lo escribimos así:
En otras palabras:
Cuando x va a infinito, 1/x va a 0
Cuando veas "límite", piensa en "acercarse"
Es una manera matemática de decir que "no estamos hablando de lo que pasa cuando x=∞, pero sabemos que cuando x crece, la respuesta se acerca más y más a 0".
Cálculo del límite en un punto
Si f(x) es una función usual (polinómicas, racionales, radicales, exponenciales, logarítmicas, etc.) y está definida en el punto a, entonces se suele cumplir que:
Es decir: para calcular el límite se sustituye en la función el valor al que tienden las x.
No podemos calcular 
porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a -2.
porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a -2.
Sin embargo si podemos calcular 
, aunque 3 no pertenezca al dominio, D= 
− {2, 3}, si podemos tomar valores del dominio tan próximos a 3 como queramos.
, aunque 3 no pertenezca al dominio, D= − {2, 3}, si podemos tomar valores del dominio tan próximos a 3 como queramos.Cálculo del límite en una función definida a trozos
En primer lugar tenemos que estudiar los límites laterales en los puntos de unión de los diferentes trozos.
Si coinciden, este es el valor del límite.
Si no coinciden, el límite no existe.
.
En x = −1, los límites laterales son:
Por la izquierda:
Por la derecha:
Como en ambos casos coinciden, existe el límite y vale 1.
En x = 1, los límites laterales son:
Por la izquierda:
Por la derecha:
Como no coinciden los límites laterales no tiene límite en x = 1
Límite de funciones. Cálculo
Propiedades.
Sean dos funciones f(x) y g(x), para las que existe límite en un punto o en el infinito. Entonces:
En general calcular el límite de una función "normal", cuando x tiende a un número real, es fácil, basta aplicar las reglas de cálculo indicadas, sustituyendo la variable independiente por el valor real al que la x tiende.
No obstante, en ocasiones, nos podemos encontrar con sorpresas, por ejemplo, que la función no esté definida para el valor en el que queremos calcular el límite . Esta situación, es habitual, cuando el límite lo queremos calcular cuando x tiende a infinito.
Una función no está definida en un punto, siempre que al intentar calcularla en ese punto, resulte alguna de las formas siguientes:
En cada caso, el límite en el punto en que la función no está determinada, dependerá de los valores que la función tome, en las proximidades de dicho punto.
Veamos como tratar cada una de estas indeterminaciones. Los métodos que se indican sirven de guía en casos parecidos.
La función no está determinada para x = 1, la razón es que el denominador se hace 0. Este tipo de indeterminaciones ocurre, cuando en el numerador y el denominador de la función, existe algún factor que se hace 0, este factor suele ser del tipo : x - valor para el que queremos calcular el límite. Si logramos eliminar, este factor del numerador y del denominador, se obtiene otra función , que toma los mismos valores en todos los puntos que no sean el punto en cuestión.
En este caso concreto, el punto es : x = 1.
La nueva función permite obtener los valores en las proximidades del punto de la indeterminación, que son los que permiten calcular el límite. En el caso concreto que nos ocupa, sería:
Cuando x crece indefinidamente, esta función es un cociente de dos cantidades que crecen indefinidamente. Se puede plantear la duda, de que si al crecer x indefinidamente, también lo hará :
puesto que sería la diferencia de dos cantidades que crecen indefinidamente, que es una indeterminación. Sacando factor común se transforma esta expresión en otra equivalente:
que crece indefinidamente, puesto que una cantidad que crece indefinidamente sigue creciendo indefinidamente aunque le restemos una cantidad constante y el producto de dos cantidades que crecen indefinidamente, también crece indefinidamente. Lo mismo ocurre con el denominador.
Como, al dividir numerador y denominador por una misma cantidad, distinta de 0, el valor de la fracción no cambia, sigue que:
Esta propiedad nos permite resolver este tipo de indeterminaciones. Se divide numerador y denominador por x, elevado al mayor de los exponentes con los que aparece en la función :
Hay un caso trivial, que ya hemos visto, sea:
Veamos ahora otra indeterminación de este tipo, pero algo más complicada:
El conjugado de una expresión, que es la diferencia de dos cantidades que crecen indefinidamente, es otra igual, excepto que en lugar de una diferencia, es una suma de dos cantidades que crecen indefinidamente. En este caso, será:
Aparece este tipo de indeterminación cuando aparecen dos funciones tales que:
Recordando un poco de álgebra:
La racionalización de radicales consiste en quitar los radicales del denominador, lo que permite facilitar el cálculo de operaciones como la suma de fracciones.
Podemos distinguir tres casos.
1Racionalización del tipo 
Se multiplica el numerador y el denominador por 
.
.
2Racionalización del tipo 
Se multiplica numerador y denominador por 
.
.
3Racionalización del tipo 
, y en general cuando el denominador sea un binomio con al menos un radical.
, y en general cuando el denominador sea un binomio con al menos un radical.
Se multiplica el numerador y denominador por el conjugado del denominador.
El conjugado de un binomio es igual al binomio con el signo central cambiado:
También tenemos que tener en cuenta que: "suma por diferencia es igual a diferencia de cuadrados".
Mi testimonio Hola a todos. Estoy aquí para testificar cómo obtuve mi préstamo del Sr. Benjamín Lee después de solicitar varias veces a varios prestamistas que prometieron ayudarme pero nunca me dieron el préstamo. Hasta que un amigo me presentó al Sr. Benjamin Lee prometió ayudarme y, de hecho, hizo lo que prometió sin ningún retraso. Nunca pensé que todavía había prestamistas fiables hasta que conocí al Sr. Benjamin Lee, que de hecho me ayudó con el préstamo y cambió mi opinión. No sé si usted necesita un préstamo genuino y urgente. No dude en contactar al Sr. Benjamin Lee a través de
ResponderBorrarWhatsApp : + 1-989-394-3740
Correo electrónico: 247officedept@gmail.com.
{ TE DESEO LOS MEJORES AMIGOS }